BIT-101

FOTD: Lerp

Lerp

The last Function Of The Day was norm, which mapped a value in a range to a value between 0 and 1. The lerp function does the exact opposite. It takes a normal value (something between 0.0 and 1.0 and maps it into a given range. That is to say it interpolates between the minimum and maximum of that range, in a straight line - linearly. Linear Interpolation = lerp.

The Code

function lerp(t, min, max) {
	return min + (max - min) * t
}

The t parameter (somewhat of a convention here) is the normal value, and min and max define the range.

Generally, t is considered to lie between 0 and 1. However, it can be smaller or larger. This will result in an output value that is outside of the range, which can actually be useful.

Once again we get the size of the range by subtracting min from max. Multiplying that by t puts you in the right place within that range. And adding that to min shifts the range so it falls in the right place. If t is zero, it will return min and if t is one, it returns max.

Example(s)

It’s often useful to think of the normal or t value as a percentage. It can be useful inside a for loop. Say you want to draw a number of shapes across the width of a canvas. You can loop from 0 to 20 and divide the iteration value by 20 to get your t. Then use that in lerp to get an x value and draw a shape at that point.

for (i = 0; i <= 20; i++) {
    t = i / 20.0
    x = lerp(t, 0, 800)
    circle(x, 50, 5)
}

Now this is a trivial example because it would be just as easy to say:

x = t * 800

But say you wanted the dots to go from some different points. Just change the 0, 800 to something else.

x = lerp(t, 100, 700)

No additional math required.

You could then lerp t to some other values like -PI to PI and then use that in a sine function.

for (i = 0; i <= 20; i++) {
    t = i / 20.0
    x = lerp(t, 0, 800)
    a = lerp(t, -PI, PI)
    y = 150 + sin(a) * 100
    circle(x, y, 5)
}

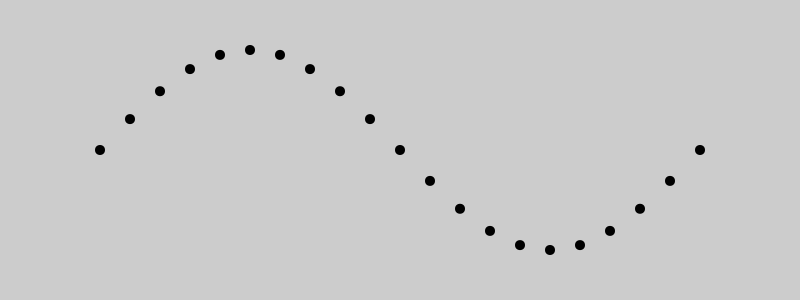
The lerp function is, all by itself, super useful, but becomes even more powerful when mixed with other useful functions. As we will see, eventually.

Resources

I did a video on this function on my Coding Math Youtube channel. View it here: Coding Math Mini #2, Linear Interpolation

Photo by Markus Spiske

Comments? Best way to shout at me is on Mastodon

Or share this post directly on Mastodon